FORMATIVE ASSIGNMENT 2

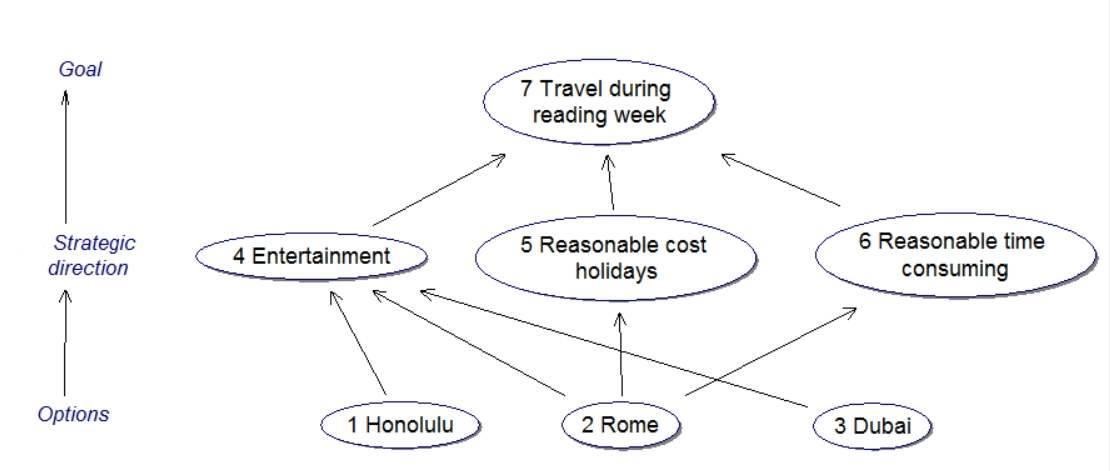
Many important decisions involve multiple objectives, and usually when there are multiple-objective decisions, it is impossible to select all of them, so instead one must find an optimized approach- an approach which provides you with the best alternative available to allocate your objectives. Let us consider the problem “Where is the best travel place?” There are three alternatives provided in this particular case, namely; Dubai, Rome and Honolulu. The ultimate goal in this scenario is to choose the best alternative based on three different objectives: cost, travel time to holiday destination and most entertaining destination.

Drawing a cognitive map for this problem requires a wide range of perspectives. A logical structure to approach this problem varies from person to person, depending on what he or she craves the most. For example; if an individual has an ample amount of money with a constraint on time for holidays, he or she would rather choose “travel time” to “cost”, as opposed to an individual who does not have much constraint on time. A similar argument holds well for a wealthy individual who has all the time in this world, in which case he or she will definitely settle on a location based on its entertainment value. However, the latter case will not be counted as a value trade off problem since the individual’s choices are sorted out, as the three objectives do not serve any purpose to him as such.

It is crucial to note that each objective may or may not have a connection with each other and each choice made has its own consequences. For example, if a person chooses cost above other objectives, then he or she needs to compromise on the time to holiday destination and may miss out on the most entertaining holiday destination. However, sometimes the odds may work in the person’s favour, in which case the holiday destination with the lowest cost might be the most entertaining, but require the longest flight duration to travel there. Here, an interesting scenario arises which can be visualized using the following example. Suppose you have a holiday destination which is cheap, but requires a long flight duration to travel there. If I assume that the time taken to arrive at the destination is directly proportional to distance, then flight cost increases significantly, but is compensated by the cheap cost of the holiday destination. Thus, this factor must be taken into consideration.

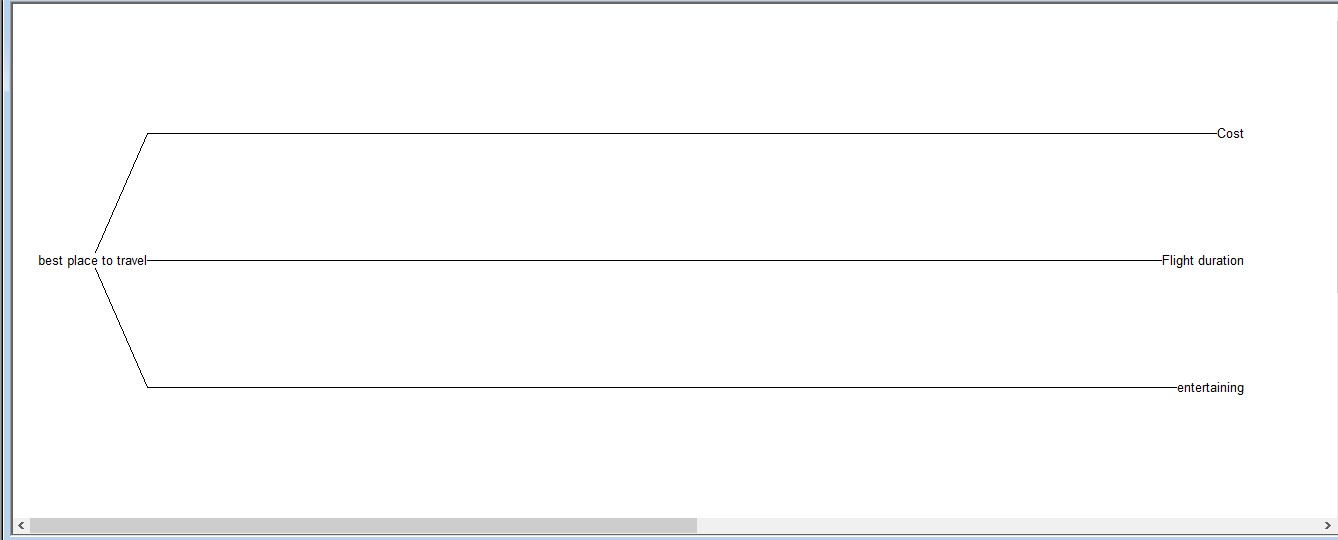
The following value tree diagram, drawn using Hiview3, focuses on the main objectives that are going to be explored.

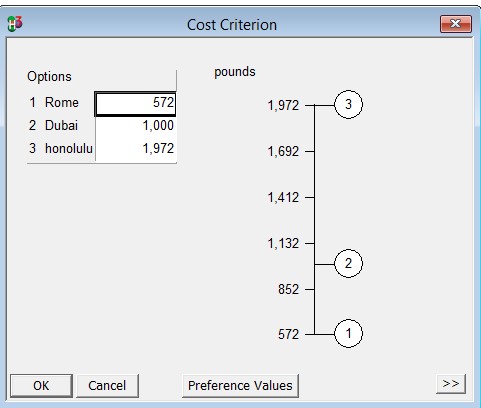
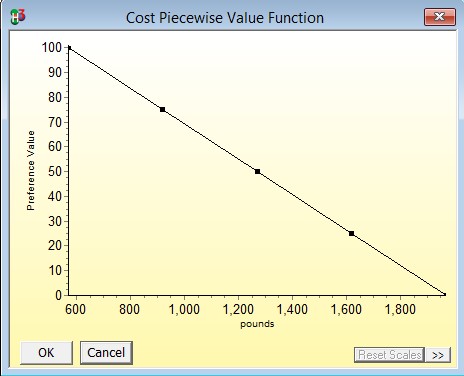
An objective is measured in terms of an attribute. In this case, different objectives have been allocated different values. As shown in the figure below, cost can be represented quantitatively by pounds.

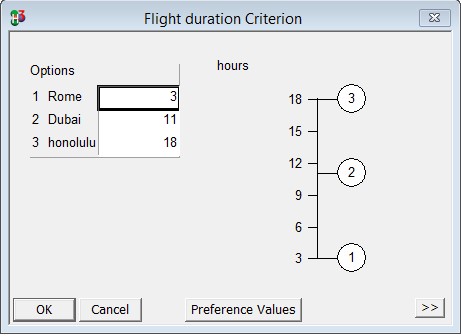
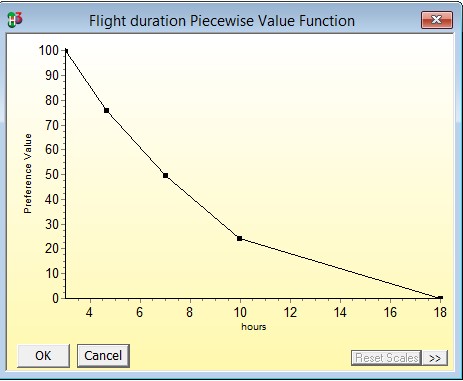
Similarly, a quantitative measure of the flight duration is the flight time to the holiday destination, measured in hours.

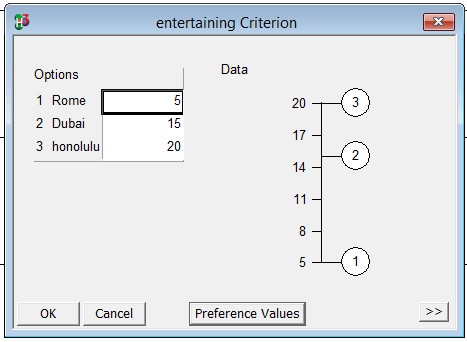
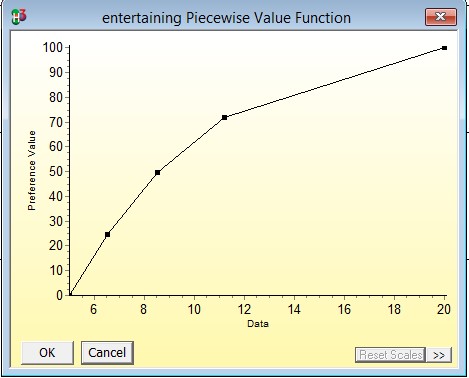
The entertainment value of a location is a qualitative term, so assigning a certain value to this variable is somewhat of a challenging task. However, this data can be obtained from various sources such as word of mouth, articles from internet, reviews from social media and personal preferences.

Changing one or more attributes can provide alternate pathways. The duration of flight can be altered depending upon connecting flights (if direct flights are not available). This will change the whole scale score and consequently the best possible alternative.

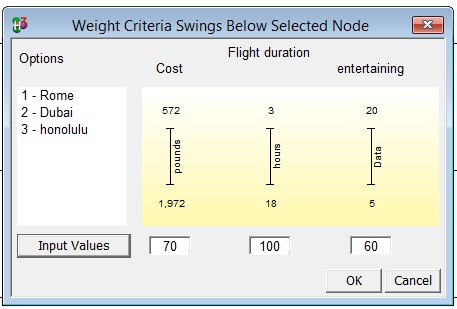
Piecewise value functions are utilised in this case which are useful approximations for normalizing continuous data. Flight Duration is an example of continuous data, as are cost and the entertainment value of a specific location. The preference value of flight duration ranges from 3 to 18 hours, the preference value of the cost function ranges from 572 to 1972 pounds, while the preference value of the entertainment value of a particular location ranges from 5 to 20.

Weighting based on the difference between the lowest and highest scores is called ‘Swing Weighting.’ The most important factor to be taken into consideration is ‘flight duration’, which is assigned a value of 100 and other factors are assigned relative to it.

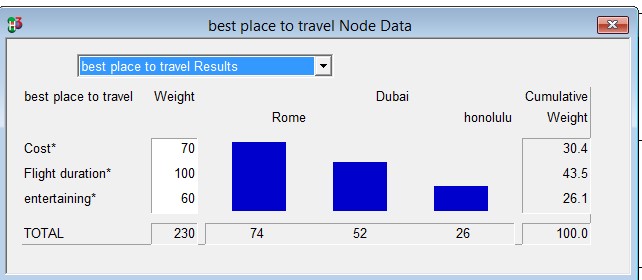
The height of the bar represents the total weighted score for that option as shown in the row beneath. Rome has a maximum value of 74, while Honolulu is the least with a value of 24. This indicates that Rome is the most preferred option, based on the analysis carried out.

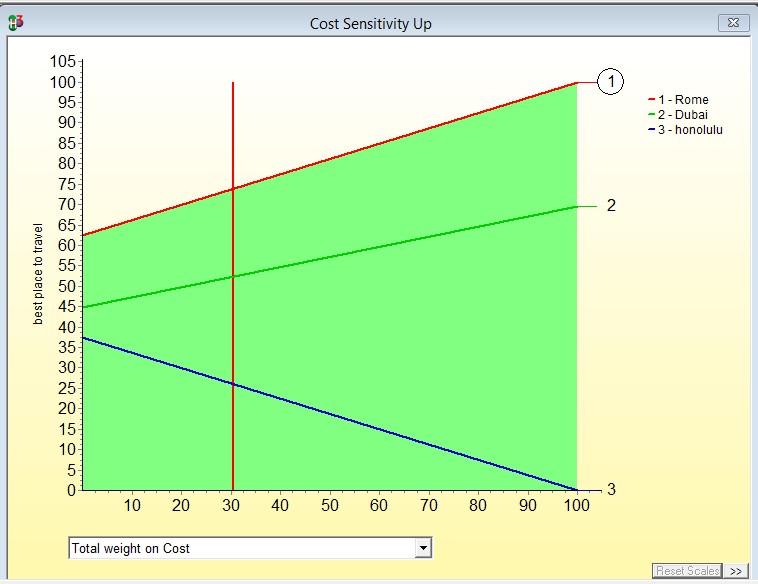
The most preferred option at any cumulative weight has the highest y-value. At the vertical red line, whichever line has the highest y-value is currently the most preferred option. It also indicates that 2 and 3 are fully dominated and will never be preferred by altering the weight on cost.

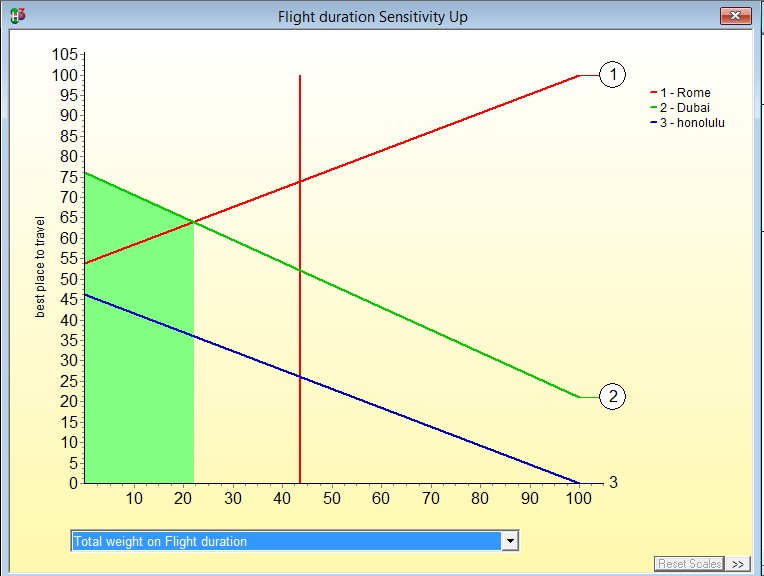
In the case of flight duration, Rome is the most preferred option unless a major change in the cumulative weights occurs

The sensitivity down window gives a summary of sensitivity throughout the whole model. The green colour indicates that the cumulative weight of “flight duration” should be decreased and “entertainment value” increased by more than 15 points, in order to alter the most preferred option to Dubai.

In conclusion, with the given attributes and weights taken into account, Rome is considered to be the most appropriate holiday destination for a decision maker to choose. However, if Rome is substituted with another alternative, then significant changes in the swing weights system should be made.